Introduction
A few months back the first, pre-CRAN versions of my nzelect package included some data from the New Zealand Census 2013. As noted in my last post, I’ve now split this into a separate nzcensus package, for ease of development and maintenance and to allow nzelect to fit within CRAN size restrictions.
The nzcensus package has a set of 60+ demographic variables aggregated at the level of meshblock, area unit, territorial authority and regional council. These variables have mostly been calculated by me from the counts in the Statistics New Zealand “meshblock” data set. For example, I’ve converted the count of individuals of European descent into a proportion of individuals who provided ethnicity information. This makes the nzcensus R package more analysis-ready than the published meshblock data because the calculated variables are suitable for comparisons across area groupings, which wasn’t the case with the straight counts.
The code that does these calculations is available on GitHub. The preparation of nzcensus is still done as part of the nzelect project, although end users can install either or both separately. I’ve fixed a few errors in my census calculations found in the past few weeks but there’s always potential for more. In the event of any uncertainty, refer back to the definitive version on the Statistics New Zealand website.
Interactive map of household income
One of the variables that I didn’t have to calculate (because it is directly available in the original data) is median household income. Here’s an interactive map showing that variable by area unit. Zoom in and out to the map in the usual way for map interaction on your device; click on circles to get the name and income value for the area unit in which it is centred. Red means higher income; blue means lower. The darkest red colour means in the top 10% of area units’ by household income.
Here’s the simple R code to create that map, drawing on the leaflet R package, which provides extremely easy to use access to the Leaflet JavaScript library:
# install the nzcensus package (note it is part of the nzelect GitHub repository):
devtools::install_github("ellisp/nzelect/pkg2")
# load up packages:
library(leaflet)
library(nzcensus)
# remove Chatham Islands
tmp <- AreaUnits2013[AreaUnits2013$WGS84Longitude > 0 & !is.na(AreaUnits2013$MedianIncome2013), ]
# create colour palette function
pal <- colorQuantile("RdBu", NULL, n = 10)
# create labels for popups
labs <- paste0(tmp$AU_NAM, " $", format(tmp$MedianIncome2013, big.mark = ","))
# draw map:
leaflet() %>%
addProviderTiles("CartoDB.Positron") %>%
addCircles(lng = tmp$WGS84Longitude, lat = tmp$WGS84Latitude,
color = pal(-tmp$MedianIncome2013),
popup = labs,
radius = 500) %>%
addLegend(
pal = pal,
values = -tmp$MedianIncome2013,
title = "Quantile of median<br>household income",
position = "topleft",
bins = 5)Modelling household income on demographic variables
In a previous post which became one of my most read posts, I had used an earlier version of this dataset to try out different validation methods for regression modelling strategies. I mentioned at the time that the modelling strategies I was using (full model, stepwise selection, dropping variance-inflating collinear variables) were less important for that particular purpose than the three different validation methods, but I think most of the take-up in comments and on Twitter showed interest in the modelling strategies.
To take this idea to its next step, I start edging towards what I think is a better modelling strategy for that data. In today’s post I start with some techniques which I think both are needed for the optimal end approach, but I don’t yet bring them together. The methods I’m using here are:
- Adding latitude and longitude as explanatory variables to adjust for the fact that spatially located observations are not independent of eachother, but spatially close variables are likely to have correlated random elements;
- Lasso, ridge regression, and elastic net regularisation (a generalisation of the lasso and ridge regression) to deal with the multicollinearity in a better way than simply dropping some of the variables;
- A generalized additive model which lets me take into account non-linear shaped relationships between some of the explanatory variables and the response variable.
My ultimate approach to this kind of regression modelling for this data - which has to wait for a later post - will combine the above, plus imputation of missing values for some explanatory variables, using the gamsel approach.
I’m going to fit three different models:
- a linear model with all explanatory variables, fit using ordinary least squares;
- a linear model with all explanatory variables, fit via elastic net regularisation which penalises for extra variables included in the model and shrinks estimated coefficients towards zero to compensate;
- a generalised additive model that lets the explanatory variables with the stronger relationship to income to have curved, non-linear relationships that better fit the actual data; and allows the nuisance spatial relationship with income to be a smooth, flexible spline.
Setup
First I load up the packages with the R functionality I’m going to need and get the data into convenient shape for this particular modelling exercise.
#===================setup=======================
library(ggplot2)
library(scales)
library(boot)
library(dplyr)
library(Hmisc) # for spearman2
library(mgcv) # for gam
library(caret) # for RMSE
library(grid)
library(stringr)
library(ggrepel)
library(glmnet)
library(maps) # for country borders on the smoothing plot
set.seed(123)
# install nzcensus if not already done
# devtools::install_github("ellisp/nzelect/pkg2")
library(nzcensus)
au <- AreaUnits2013 %>%
# drop the columns with areas' code and name, and the redundant coordinate system
select(-AU2014, -AU_NAM, -NZTM2000Easting, -NZTM2000Northing) %>%
# drop some intrinsically collinear variables that would be exactly collinear
# if it weren't for rounding error and confidentialisation:
select(-PropWorked40_49hours2013, -Prop35to39_2013, -PropFemale2013)
# give meaningful rownames, helpful for some diagnostic plots later
row.names(au) <- AreaUnits2013$AU_NAM
# remove some repetition from the variable names
names(au) <- gsub("_2013", "", names(au))
names(au) <- gsub("2013", "", names(au))
names(au) <- gsub("Prop", "", names(au))
# restrict to areas with no missing data. An improvement for later
# is to use imputation and include this step within the validation.
au <- au[complete.cases(au), ]
# give the data a generic name for ease of copying and pasting
the_data <- au
# we need a dummy variable for the Chathams because it's extreme value of longitude
# makes any spatial variables otherwise highly problematic.
# the_data$chathams <- the_data$WGS84Longitude < 100
the_data <- the_data[the_data$WGS84Longitude > 100, ]
names(the_data) <- make.names(names(the_data))Linear model
My first and simplest method is one of those I used in the previous post: linear regression, estimated with ordinary least squares, using all the explanatory variables.
In comparing these approaches I am always going to use the same validation approach. All three validation methods gave similar results, so I’m going to pick one that’s easy to generalise, the so-called “simple bootstrap” validation method. In this approach, a re-sample of data is taken from the original data with replacement, the same number of rows as originally (hence some points sampled twice, some not at all). The model is fit based on this re-sample, and that model fit is used to predict the response variable for the entire original dataset (not just the “out of bag” samples - that’s a different approach). I collect the average root mean square error of those predictions from doing this resampling 99 times.
Because this classic model forms a reference point for alternative methods, it’s important to consider the classic diagnostic graphics too. Here they are:
There’s no problems with outliers or leverage (noting that in the earlier preparation code I’d excluded the Chatham Islands from the dataset to make the spatial aspect of the problem tractable). There’s a bit of curvature in the residuals, indicating a possible structural problem that later on we will use the generalized additive model to address. There’s also some non-normality in the residuals - the QQ plot (top right of the four) shows that towards the upper and lower extremes of the residuals’ distribution the actual values of standardized residuals are larger in absolute magnitude than the theoretical values they should have from a Normal distribution. This isn’t disastrous, but it does mean we need to take care in inference, and use methods such as the bootstrap for all of our inference as methods that rely on distributional assuptions will be suspect.
Here’s the code for fitting this simple model. As will be the case for all three of our approaches, we start by defining a function that
- fits the model to a resample with replacement of the data, defined by the argument
i; - uses that model to predict the values of income from the full original data;
- returns the root mean square errors of those predictions.
This function can then be used by the boot function to perform the bootstrap validation.
fit_lm <- function(data, i){
mod1 <- lm(MedianIncome ~ ., data = data[i, ])
# use the model based on resample on the original data to estimate how
# good or not it is:
RMSE(predict(mod1, newdata = data), data$MedianIncome)
}
# use bootstrap validation for an unbiaased estimate of root mean square error
rmses_lm_boot <- boot(the_data, statistic = fit_lm, R = 99)
lm_rmse <- mean(rmses_lm_boot$t)
# save a single version of this model for later
mod_lm <- lm(MedianIncome ~ ., data = the_data)
# Check out classic diagnostic plots:
par(mfrow = c(2, 2))
plot(mod_lm)The average bootstrapped root mean square error from this method is 2015.
Elastic net regularization
Elastic net regularization is a generalisation of the “ridge regression” and “lasso” methods of estimating parameters of a linear model. Both ridge regression and lasso estimation provide extra penalties for the magnitude of coefficients in the linear predictor; the “lasso” penalises based on the sum of the absolute value of estimated coefficients, and the “ridge” penalises based on the sum of squared values. In both cases the net effect is to shrink estimated coefficients towards zero. It’s a far superior method for model building than dropping variables based on their variable inflation factors, or stepwise regression, the two methods I used for demonstration purposes in my previous posts. In particular, all sorts of problems for subsequent inference, such as bias towards significance of the parameters remaining in the model, are reduced or eliminated altogether.
The elastic net approach is defined by two hyperparameters, alpha and lambda. When alpha = 1 the elastic net is equivalent to the lasso; when alpha = 0 it is equivalent to ridge regression. For any given value of alpha, the value of lambda indicates how much penalty is given to the size of coefficients in the linear predictor. The cv.glmnet function uses cross validation to give the best value of lambda for any given alpha; a bit of extra work is needed to simultaneously choose alpha. In the code below I use cv.glmnet with nine different values of alpha:
# A lasso, ridge rigression, or elastic net (which combines the two) is a way
# of dealing with the collinearity by forcing some coefficients to shrink (possibly to zero)
# while doing minimal damage to the inferential qualities of the rest and to the overall model fit.
# First we need to decide between ridge regression and lasso or elastic net (between the two)
# define folds for cross validation so can check the impact of different values of alpha
set.seed(124)
foldid <- sample(1:10, nrow(the_data), replace = TRUE)
# separate out the explanatory from response variable
# for when using lasso and ridge regression
X <- the_data %>% select(-MedianIncome)
Y <- the_data$MedianIncome
cv_results <- data_frame(lambda = numeric(), alpha = numeric(), mcve = numeric())
alphas <- seq(from = 0, to = 1, length.out = 9)
for(i in alphas){
cvfit <- cv.glmnet(as.matrix(X), Y, foldid = foldid, alpha = i)
tmp <- data_frame(lambda = cvfit$lambda, alpha = i, mcve = cvfit$cvm)
cv_results <- rbind(cv_results, tmp)
}
arrange(cv_results, mcve)
# best alpha with this see is 0.75 but right combination of alpha and lambda
# works pretty well for any alpha
# For the graphic I take square root of mcve so it is back on same scale as RMSE used elsewhere in this post
ggplot(cv_results, aes(x = lambda, y = sqrt(mcve), colour = as.factor(round(alpha, 3)))) +
geom_line(size = 2) +
geom_line(size = 0.2, colour = "grey50", aes(group = as.factor(round(alpha, 3)))) +
scale_x_log10() +
coord_cartesian(ylim = c(1800, 4000), xlim = c(5, 1000)) +
scale_colour_brewer("alpha", palette = "Greens", guide = guide_legend(reverse = TRUE)) +
ggtitle("Cross-validation to select hyper parameters\nin elastic net regression") +
scale_y_continuous("Square root of mean cross validation error", label = comma) +
theme(legend.position = "right")Here’s the results in tabular form. Many combinations of alpha and lambda work well. Basically, there’s not much to choose from between ridge regression and lasso with this particular set of data, which has a nice moderate size of observations for a modest number of variables.
> arrange(cv_results, mcve)
Source: local data frame [740 x 3]
lambda alpha mcve
<dbl> <dbl> <dbl>
1 6.029743 0.750 4290529
2 5.168351 0.875 4291482
3 4.963227 1.000 4291871
4 7.235692 0.625 4291920
5 7.941163 0.625 4292204
6 6.592893 0.625 4292411
7 4.290856 0.875 4292494
8 4.522307 1.000 4292497
9 6.617636 0.750 4292529
10 5.672259 0.875 4292609
.. ... ... ...Here’s the graphic presentation of those results, making it clearer that for an appropriate value of lambda, pretty much any alpha gives an ok result.
Choosing 0.750 as the value of alpha and using cross-validation for each resampled dataset to choose lambda, we can now use bootstrap validation to check out the results of this modelling approach.
fit_elastic <- function(data, i){
# i = sample(1:nrow(data), nrow(data), replace = TRUE)
Y_orig <- data$MedianIncome
X_orig <- as.matrix(select(data, -MedianIncome))
data2 <- data[i, ]
Y_new <- data2$MedianIncome
X_new <- as.matrix(select(data2, -MedianIncome))
lambda <- cv.glmnet (X_new, Y_new, alpha = 0.85)$lambda.min
mod1 <- glmnet(X_new, Y_new, lambda = lambda, alpha = 0.85)
# use the model based on resample on the original data to estimate how
# good or not it is:
rmse <- RMSE(predict(mod1, newx = X_orig), Y) return(rmse)
}
rmses_elastic_boot <- boot(data = the_data, statistic = fit_elastic, R = 99) # takes a few minutes
elastic_rmse <- mean(rmses_elastic_boot$t)The average bootstrapped root mean square error from this method is again 2015, showing that the improved estimates of individual coefficients has neither worsened nor improved the overall fit.
The characteristic of shrinkage methods is that the estimates of coefficients in the linear predictor are less in absolute size than are the ordinary least squares estimators. The relatively mild nature of this phenomenon in this particular case is shown in the graphic below. The straight diagonal line shows where the shrunk estimate of the coefficient from the elastic net equals that from ordinary least squares; when points are to the right of this line if positive, or to the left of it if negative, the elastic net regularized estimate is closer to zero than its ordinary least squares equivalent. The shrinkage is pretty mild.
Generalized additive model
The third and final strategy to be tried today is a different structural model, allowing non-linear relations between the explanatory variables and the response (median household income) they are trying to predict. It turns out this has a fairly material impact on overall model fit. I’ll start with a plot showing those non-linear relations for the fifteen demographic variables most closely related to household income and the two spatial (latitude and longitude) variables:
We can see a bit of curve in some of these relationships. For example, the relationship between the proportion of people who are partnered and income is decidedly non-linear, with an upwards surge in income for a small number of low-partnership areas that belies the general positive correlation. The relationship between the proportion of people in full time employment and income shows a definite S shape. The relationship between the proportion of people with Bachelors degrees and income gets steeper as the proportion gets higher; and so on.
The latitude and longitude plot at the bottom right of the image above is the most complex non-linear relationship and the plot is a little difficult to see, so here’s an enhanced version of it:
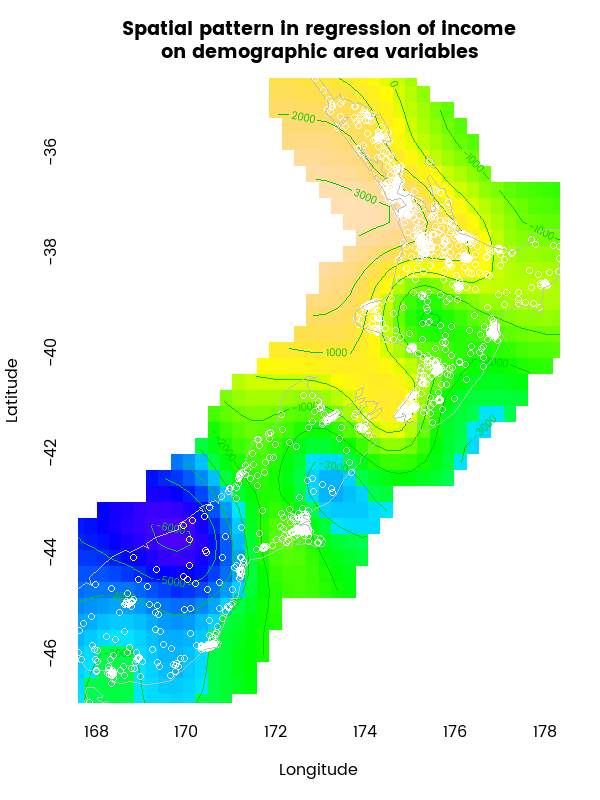
This map is showing the relationship between location and income, after all the demographic variables are accounted for. Including a flexible spline for an interaction between longitude and latitude in a Generalized Additive Model like this is a good way of controlling for the nuisance factor of spatial autocorrelation, which if not accounted for is likely to lead to false inference, with the strength of evidence for relations between the data being overestimated (apparent relations can be just artefacts of how the spatial grouping was made).
In specifying models of this sort I often follow Frank Harrell’s informal advice of first determining how many degrees of freedom are available (between 1/20 and 1/10 the number of observations). Those degrees of freedom are then allocated to the various explanatory variables in the form of splines, with more degrees of freedom meaning a flexible curved relationship with income is possible and a single degree of freedom meaning a straight linear relationship. The explanatory variables with the strongest non-parametric relationship with the response variable get more degrees of freedoms. This approach works only after the analyst has made a commitment to include all examined variables in the model; letting the strength of relationship with the response determine whether an explanatory variable gets in at all is a form of stepwise regression and subject to all the problems that come from that.
To estimate the strength of the non parameteric relationships I use Harrell’s spearman2 which regresses Y on the rank of X and the square of the rank of X. This powerful method allows non-monotonic relationships between variables. In the case of today’s data, it shows the strongest relationship to household income as being the proportion of people in full time employment, households with access to the internet, and so on as seen in the output below:
> sp <- spearman2(MedianIncome ~ ., data = the_data)
> sp[order(-sp[ ,6])[1:15], ]
rho2 F df1 df2 P Adjusted rho2 n
FullTimeEmployed 0.7134528 4436.8712 1 1782 0 0.7132920 1784
InternetHH 0.5844727 2506.5272 1 1782 0 0.5842396 1784
NoQualification 0.4477222 1444.6370 1 1782 0 0.4474123 1784
UnemploymentBenefit 0.4309570 1349.5736 1 1782 0 0.4306377 1784
Smoker 0.4103768 1240.2690 1 1782 0 0.4100459 1784
Partnered 0.3866804 1123.5000 1 1782 0 0.3863363 1784
Managers 0.3854615 1117.7367 1 1782 0 0.3851166 1784
Bachelor 0.3729497 1059.8773 1 1782 0 0.3725978 1784
SelfEmployed 0.3666249 1031.4988 1 1782 0 0.3662695 1784
NoMotorVehicle 0.3587586 996.9846 1 1782 0 0.3583987 1784
Unemployed 0.3572286 990.3698 1 1782 0 0.3568679 1784
Labourers 0.3387476 912.8864 1 1782 0 0.3383766 1784
Worked50_59hours 0.3311916 882.4404 1 1782 0 0.3308163 1784
Separated 0.3122393 809.0175 1 1782 0 0.3118533 1784
Maori 0.3022017 771.7465 1 1782 0 0.3018101 1784I then allocate flexible splines to the first 15 or so of those variables. The 4 x 4 grid of non-linear plots and the map of spatial effects that began this section was produced with the code below:
# see http://stackoverflow.com/questions/30627642/issue-with-gam-function-in-r
# for why the data needs to be specified in both terms() and in gam()
the_formula <- terms(MedianIncome ~
s(FullTimeEmployed, k = 6) +
s(InternetHH, k = 6) +
s(NoQualification, k = 5) +
s(UnemploymentBenefit, k = 5) +
s(Smoker, k = 5) +
s(Partnered, k = 5) +
s(Managers, k = 4) +
s(Bachelor, k = 4) +
s(SelfEmployed, k = 4) +
s(NoMotorVehicle, k = 4) +
s(Unemployed, k = 3) +
s(Labourers, k = 3) +
s(Worked50_59hours, k = 3) +
s(Separated, k = 3) +
s(Maori, k = 3) +
s(WGS84Longitude, WGS84Latitude) +
.,
data = the_data)
gam_model <- gam(the_formula, data = the_data)
# grid of nonlinear relations
par(bty = "l", mar = c(5,4, 2, 1))
plot(gam_model, residuals = TRUE, pages = 1, shade = TRUE,
seWithMean = TRUE, ylab = "")
grid.text("Impact of area average variables on median income by area unit (New Zealand census 2013)", 0.5, 0.99,
gp = gpar(fontfamily = "myfont"))
# map of spatial impacts
par(bty = "l", family = "myfont", fg = "white")
plot(gam_model, shade = TRUE, select = 16, rug = TRUE, se = FALSE, scheme = 2, col = topo.colors(100),
pch = 1, ylab = "Latitude", xlab = "Longitude", main = "Spatial pattern in regression of income\non demographic area variables")
map(add = TRUE, col = "grey75")The bootstrap validation of this method is straightforward and follows the same pattern as the two previous methods:
fit_gam <- function(data, i){
mod1 <- gam(the_formula, data = data[i, ])
# use the model based on resample on the original data to estimate how
# good or not it is:
RMSE(predict(mod1, newdata = data), data$MedianIncome)
}
rmses_gam_boot <- boot(data = the_data, statistic = fit_gam, R = 99) # takes a few minutes
gam_rmse <- mean(rmses_gam_boot$t)The root mean square error from this method is 1728, a very material improvement in model performance; much less than 2015.
The spatial spline (which was allowed to be as flexible as it needed) uses 27 effective degrees of freedom and the other splines another 30 (plus 60 or so from the parametric effects), taking this model to the most flexibility reasonable from the 1775 data points.
Conclusions
Here’s those overall results:
> data.frame(lm_rmse, elastic_rmse, gam_rmse)
lm_rmse elastic_rmse gam_rmse
1 2015.34 2014.871 1728.254The elastic net approach gives us more confidence in the estimates of individual coefficients but in this case does not materially improve model performance. Allowing curvature in the relations improved the model but does not address the collinearity problems.
As foreshadowed earlier, the next improvements to make will be to combine these two methods - elastic net regularization for feature selection and shrinkage, and generalized additive models to allow non-linear relationships. The gamsel R package enables this and I’ll return to it in a later post; perhaps at the same time as addressing an improved method of dealing with missing data (imputation rather than dropping altogether).
For now, this serves as a sequel to my earlier piece on model validation, turning the attention now onto model strategies themselves; and to demonstrate a taster of the uses the nzcensus package can be turned to.
The nzcensus package is still experimental, use with caution. Please file bugs or enhancement requests as issues on GitHub.



